Judul : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPLTV
link : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPLTV
Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPLTV
Masih ingatkah kalian mengenai sistem persamaan dua variabel? Sistem persamaan linear dua variabel adalah sistem persamaan yang memuat dua variabel. Sistem persamaan ini dapat diselesaiakan dengan metode grafik, eliminasi, substitusi, dan kombinasi.
Pada materi ini kita akan mempelajari sistem persamaan linear tiga variabel. Hampir sama dengan sistem persamaan linear dua variabel, sistem persamaan linear tiga variabel adalah suatu sistem persamaan yang memuat tiga variabel.
Perhatikan contoh berikut :
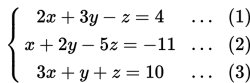
Penyelesaian dari sistem persamaan ini adalah pasangan berurut yang memenuhi setiap persamaan linear pada sistem persamaan tersebut. Sebagai contohnya, (2,1,3) merupakan penyelesaian dari sistem persamaan linear di atas.
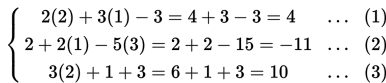
Metode kombinasi pada penyelesaian sistem persamaan dua variabel dapat digunakan untuk menyelesaikan sistem persamaan linear tiga variabel dengan langkah sebagai berikut :
Mari kita perhatikan contoh berikut!
Contoh 1 : Menggunakan Metode Kombinasi Linear
Selesaikan sistem persamaan berikut!
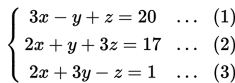
Pembahasan
(1) Dengan mengeliminasi variabel y dari persamaan (1) dan (2) diperoleh:
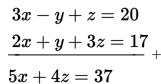
Selanjutnya, dengan mengalikan persamaan (2) dengan 3 dan mengeliminasi variabel y dengan persamaan (3), diperoleh :
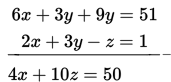
(2) Dengan melakukan eliminasi pada 2 persamaan linear yang baru, maka diperoleh :
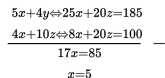
Selanjutnya, dengan melakukan substitusi x = 5 ke salah satu persamaan sehingga diperoleh z = 3.
(3) Dengan melakukan substitusi x = 5 dan z = 3 ke salah satu persamaan awal, diperoleh :
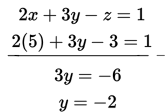
Jadi, penyelesaian sistem persamaan ini adalah , , dan atau dapat dituliskan dalam bentuk pasangan berurut.
Contoh 2 : Menyelesaikan sistem persamaan yang tidak mempunyai penyelesaian
Selesaikan sistem persamaan linear berikut ini!
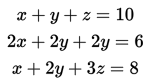
Pembahasan
Untuk menyelesaikan sistem persamaan di atas, kalikan persamaan pertama dengan 2 kemudian eliminasi dengan persamaan kedua.
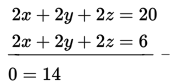
Perhatikan bahwa sistem persamaan ini menghasilkan persamaan yang salah sehingga dapat disimpulkan bahwa sistem persamaan tersebut tidak mempunyai penyelesaian.
Contoh 3 : Menyelesaikan sistem persamaan yang mempunyai banyak penyelesaian
Selesaikan sistem persamaan berikut ini!

Pembahasan
Untuk menyelesaikan sistem persamaan linear di atas, ikutilah langkah-langkah berikut ini :
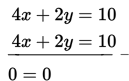
Sistem persamaan ini menghasilkan identitas 0 = 0 sehingga sistem persamaan tersebut mempunyai banyak penyelesaian.
Pada materi ini kita akan mempelajari sistem persamaan linear tiga variabel. Hampir sama dengan sistem persamaan linear dua variabel, sistem persamaan linear tiga variabel adalah suatu sistem persamaan yang memuat tiga variabel.
Perhatikan contoh berikut :
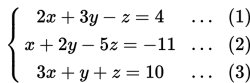
Penyelesaian dari sistem persamaan ini adalah pasangan berurut yang memenuhi setiap persamaan linear pada sistem persamaan tersebut. Sebagai contohnya, (2,1,3) merupakan penyelesaian dari sistem persamaan linear di atas.
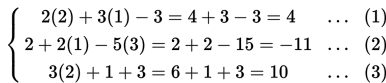
Metode kombinasi pada penyelesaian sistem persamaan dua variabel dapat digunakan untuk menyelesaikan sistem persamaan linear tiga variabel dengan langkah sebagai berikut :
- Gunakan metode kombinasi linear untuk mengubah sistem persamaan linear tiga variabel menadi sistem persamaan linear dua variabel.
- Selesaikan sistem persamaan linear yang baru untuk menemukan penyelesaian kedua variabel.
- Substitusikan hasil yang diperoleh pada langkah (2) ke salah satu persamaan untuk memperoleh penyelesaian yang belum diketahui.
Mari kita perhatikan contoh berikut!
Contoh 1 : Menggunakan Metode Kombinasi Linear
Selesaikan sistem persamaan berikut!
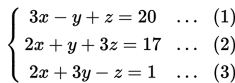
Pembahasan
(1) Dengan mengeliminasi variabel y dari persamaan (1) dan (2) diperoleh:
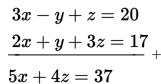
Selanjutnya, dengan mengalikan persamaan (2) dengan 3 dan mengeliminasi variabel y dengan persamaan (3), diperoleh :
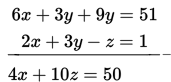
(2) Dengan melakukan eliminasi pada 2 persamaan linear yang baru, maka diperoleh :
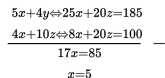
Selanjutnya, dengan melakukan substitusi x = 5 ke salah satu persamaan sehingga diperoleh z = 3.
(3) Dengan melakukan substitusi x = 5 dan z = 3 ke salah satu persamaan awal, diperoleh :
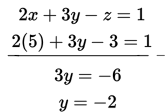
Jadi, penyelesaian sistem persamaan ini adalah , , dan atau dapat dituliskan dalam bentuk pasangan berurut.
Contoh 2 : Menyelesaikan sistem persamaan yang tidak mempunyai penyelesaian
Selesaikan sistem persamaan linear berikut ini!
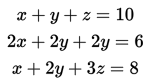
Pembahasan
Untuk menyelesaikan sistem persamaan di atas, kalikan persamaan pertama dengan 2 kemudian eliminasi dengan persamaan kedua.
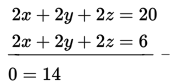
Perhatikan bahwa sistem persamaan ini menghasilkan persamaan yang salah sehingga dapat disimpulkan bahwa sistem persamaan tersebut tidak mempunyai penyelesaian.
Contoh 3 : Menyelesaikan sistem persamaan yang mempunyai banyak penyelesaian
Selesaikan sistem persamaan berikut ini!

Pembahasan
Untuk menyelesaikan sistem persamaan linear di atas, ikutilah langkah-langkah berikut ini :
- Kurangkan (1) dan (2) sehingga diperoleh 2x + y = 5 ………………… (4)
- Jumlahkan persamaan (2) dan (3) sehingga diperoleh 4x + 2y = 10 …(5)
- Kalikan persamaan (4) dengan 2 kemudian eliminasi
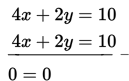
Sistem persamaan ini menghasilkan identitas 0 = 0 sehingga sistem persamaan tersebut mempunyai banyak penyelesaian.
Demikian Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPLTV
Sekianlah postingan Artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPLTV kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Penyelesaian SPLTV dengan alamat link https://metodekuadrat.blogspot.com/2016/06/sistem-persamaan-dan-pertidaksamaan_47.html