Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi - Hallo semua metode kuadrat, Pada Postingan kali ini yang berjudul Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi, telah kami persiapkan dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Matematika, ini dapat anda pahami. dan bermanfaat, selamat membaca.

Judul : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi
link : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi

Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi

Salah satu keterampilan yang sangat penting dalam bidang matematika adalah kemampuan untuk menafsirkan dan memahami grafik. Dalam pelajaran ini, kita akan melihat beberapa ciri-ciri pokok grafik, termasuk interval penamaan yang menentukan apakah suatu grafik merupakan positif atau negatif, mencari perpotongan sumbu x dan y dalam sebuah grafik, mencari nilai maksimum dan minimum dari sebuah grafik, dan menentukan apakah suatu grafik mempunyai fungsi naik atau turun.

Manakah fungsi positif dan manakah yang negatif itu?
Secara grafis, nilai fungsi f(x), sama dengan nilai y. Sebuah fungsi dikatakan positif jika koordinat y bernilai positif (diatas sumbu x x), dan dikatakan negatifjika koordinat y bernilai negatif (di bawah sumbu x). Jika kalian ditanya apakah suatu fungsi merupakan fungsi positif atau negatif, maka kalian tinggal memperhatikan sumbu x, yang memnentukan apakah suatu grafik merupakan grafik positif atau negatif.


Contoh 1         
Nyatakan interval dimana fungsi f(x) bernilai negatif.

Fungsi ini adalah negatif selama kurva tersebut memiliki nilai y negatif. Jadi, fungsi tersebut adalah negatif jika x adalah kurang dari 3 dan juga jika x adalah antara -1 dan 3. 3Perhatikan contoh penulisan interval berikut ini:
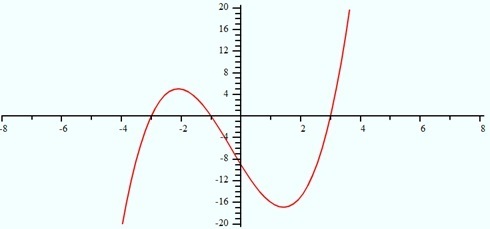
x: x < -3 and -1 < x < 3
atau
x: (-∞, -3)U(-1, 3)

Nilai maksimum dan minimum dari suatu fungsi
Titik maksimum mutlakadalah titik dalam sebuah fungsi yang mempunyai nilai y tertinggi. Titik minimum mutlak adalah titik dalam sebuah fungsi yang mempunyai nilai y terendah. Kadang-kadang kalian akan diminta untuk mencari nilai maksimum lokal atau disebut juga nilai minimum – Nilai maksimum lokal adalah titik di mana fungsi mencapai titik tinggi atau rendah relatif terhadap titik-titik di sekitarnya.

Titik potong sumbu x dan y
Titik potong sumbu x dari suatu fungsi adalah titik di mana sebuah fungsi memotong sumbu x. Ini disebut penyelesaian sebuah fungsi. (Jika fungsi tersebut ditetapkan sama dengan nol, nilai-nilai ini disebut akar dari persamaan, dan merupakan penyelesaian dari persamaan itu.) Sebuah fungsi dapat memiliki 0 , 1, atau lebih titik potong sumbu x

Titik potong sumbu y adalah titik di mana suatu fungsi melintasi sumbu y. Sebuah fungsi hanya dapat memiliki satu titik potong sumbu y.

Fungsi naik dan turun
Sebuah fungsi dikatakan naiknaik jika nilai y dalam suatu fungsi semakin besar, seiring nilai x yang juga membesar. Sebuah fungsi dikatakan turunjika nilai y semakin kecil, seiring dengan nilai x yang membesar. Cara mudah untuk memahaminya adalah dengan menelusuri kurva dari kiri ke kanan, jika pensil kita bergerak meningkat maka kurva tersebut dikatakan meningkat, dan jika pensil kita bergerak menurun maka kurva tersebut dikatakan menurun.


Contoh 2
Untuk fungsi berikut,
(a) Tentukan maksimum lokal dan nilai-nilai minimum
(b) Tentukan titik maksimum mutlak dan titik minimum mutlak
(c) Tentukan interval di mana fungsi ini menjadi naik dan turun.
(d) Tentukan perpotongan sumbu x- dan y
(e) Nyatakan interval di mana fungsinya adalah positif dan negatif.

(a) ) Terdapat 1 nilai maksimum lokal di sekitar x = -0.5. Terdapat sebuah nilai minimum lokal dari kurang lebih -7 pada x = sekitar -2.5, dan minimum lokal yang lain adalah dari sekitar -1.5 pada x = 0.5.

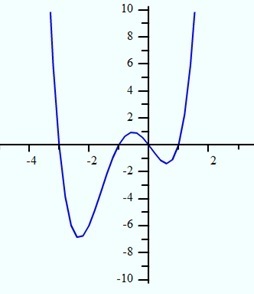
(b) Titik minimum absolut adalah sekitar -7, jika x = sekitar -2.5. Tidak ada nilai maksimum absolut karena grafik terus meningkat pada kedua ujungnya.

(c) (c) Fungsi ini meningkat pada interval x:(-2.5, -0.5)U(0.5,∞).
     Fungsi ini menurun pada interval x:(-∞, -2.5)U(-0.5, 0.5).

(d) Titik potong sumbu x adalah -3, -1, dan 1. Titik potong sumbu y adalah 0.

(e) Fungsi ini merupakan positif pada x:(-∞, -3)U (-1, 0)U(1,∞).
      Fungsi ini merupakan negatif pada x:(-3, -1)U(0, 1).

Demikian Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi

Sekianlah postingan Artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih

Anda sekarang membaca artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Menggunakan Fitur Kunci Untuk Menggambar Fungsi dengan alamat link https://metodekuadrat.blogspot.com/2016/06/sistem-persamaan-dan-pertidaksamaan_22.html