Judul : Relasi dan Fungsi: Menginterpretasikan dan Menggambar Grafik Fungsi dari Soal Cerita
link : Relasi dan Fungsi: Menginterpretasikan dan Menggambar Grafik Fungsi dari Soal Cerita
Relasi dan Fungsi: Menginterpretasikan dan Menggambar Grafik Fungsi dari Soal Cerita
Apakah sebuah fungsi merupakan sebuah relasi?
Relasi merupakan sebuah korespondensi antara dua buah himpunan. Jika x dan y masing-masing merupakan dua elemen dari suatu himpunan dan jika terdapat sebuah relasi antara x dan y, maka dapat kita katakan bahwa x berkorespondensi dengan y atau y bergantung pada x :
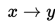
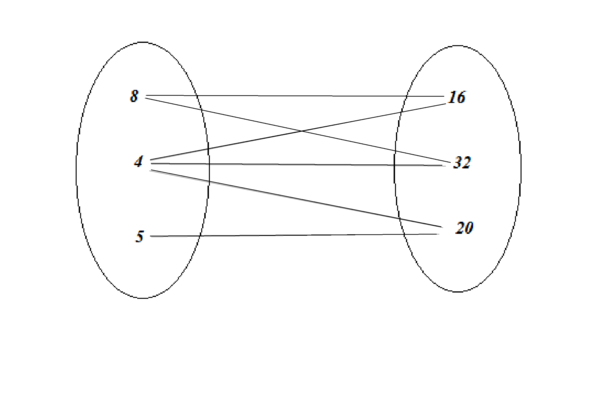
Adapun fungsi merupakan relasi dimana setiap elemen dalam domain mempunyai tepat satu pasangan dalam kodomain. Gambar berikut ini merupakan contoh sebuah fungsi :
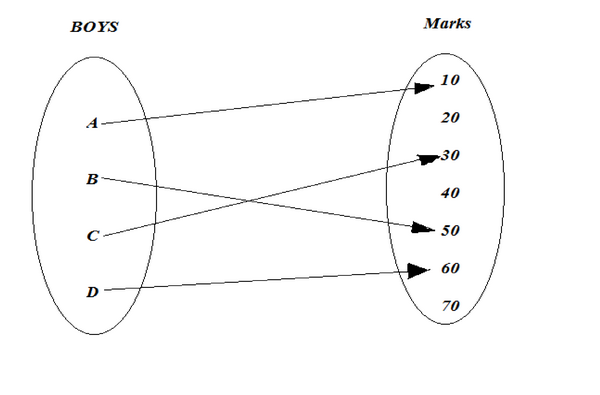
semua fungsi merupakan relasi, akan tetapi tidak semua relasi merupakan fungsi.
Sebuah fungsi dapat dinyatakan sebagai sebuah himpunan
pasangan berurutan, dalam bentuk tabel, dalam bentuk grafik, atau dinyatakan sebagai sebuah persamaan linear
atau non linear.
Dalam sebuah fungsi, setiap x dalam domain mempunyai tepat satu pasangan y dalam range (daerah hasil). Dengan kata lain, sebuah grafik fungsi tidak memuat titik dengan absis (x) yang sama tetapi ordinat (y) berbeda.
Grafik fungsi biasa digunakan untuk menggambarkan hubungan antara suatu model fungsi dan untuk memanipulasi bentuk matematika dari sebuah fungsi sehingga diperoleh sifat-sifat dari fungsi tersebut.
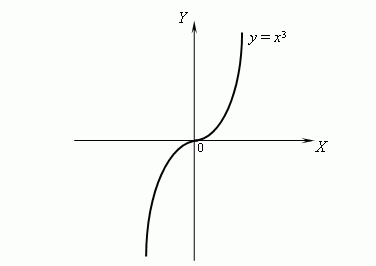
Contoh fungsi dalam konteks
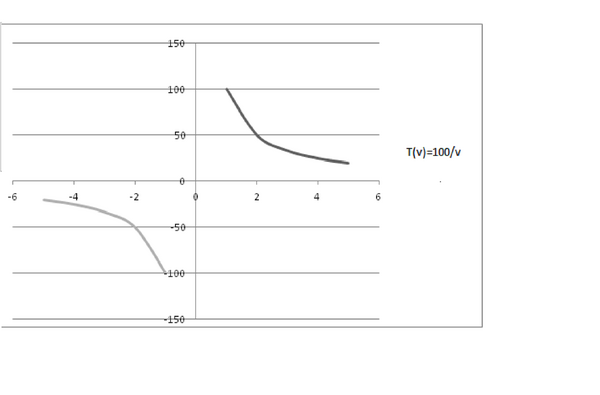
Waktu (dalam jam) yang dibutuhkan oleh sebuah mobil untuk bergerak sejauh 100 mil merupakan sebuah fungsi kecepatan mobil dalam mil per jam (v). Dalam hal ini, T(v) = 100/v menyatakan hubungan antara jarak yang ditempuh mobil dengan kecepatan mobil tersebut. Grafik berikut ini merupakan grafik dari fungsi T di atas :
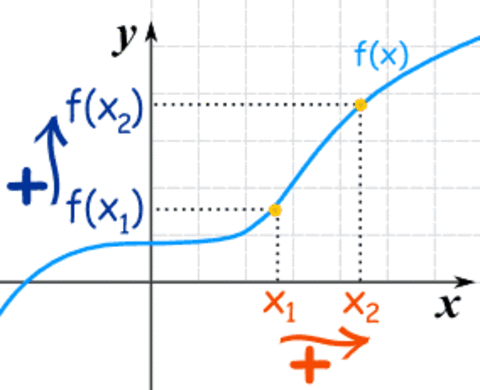
Fungsi f dikatakan naik dalam interval terbuka I jika untuk sebarang x1 dan x2 dalam I, dimana x1<x2, berlaku : f(x1)<f(x2). Perhatikan grafik berikut ini :
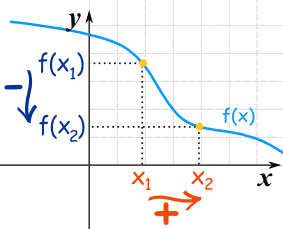
Perhatikan grafik berikut ini :
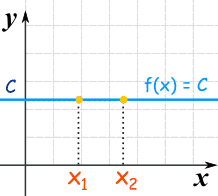
Perhatikan grafik berikut ini :
Keliling dari sebuah persegi panjang adalah 50 kaki. Nyatakan luas persegi panjang tersebut sebagai fungsi dari ppanjangnya!
Penyelesaian
Berdasarkan soal di atas,
2p + 2l= 50
p+l= 25
l=25-l
Dengan demikian,
L= p*l
L=p(25-p)
Selanjutnya, dengan menuliskan luas dalam p, maka diperoleh :
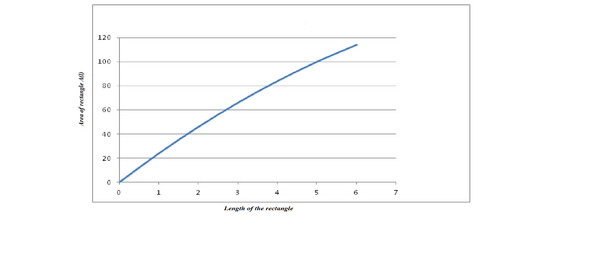
L(p)= p(25-p)
Adapun grafik fungsi dari soal di atas adalah sebagai berikut :
Demikian Relasi dan Fungsi: Menginterpretasikan dan Menggambar Grafik Fungsi dari Soal Cerita
Sekianlah postingan Artikel Relasi dan Fungsi: Menginterpretasikan dan Menggambar Grafik Fungsi dari Soal Cerita kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel Relasi dan Fungsi: Menginterpretasikan dan Menggambar Grafik Fungsi dari Soal Cerita dengan alamat link https://metodekuadrat.blogspot.com/2016/06/relasi-dan-fungsi-menginterpretasikan.html