Relasi dan Fungsi: Grafik fungsi linier dan kuadrat - Hallo semua metode kuadrat, Pada Postingan kali ini yang berjudul Relasi dan Fungsi: Grafik fungsi linier dan kuadrat, telah kami persiapkan dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Matematika, ini dapat anda pahami. dan bermanfaat, selamat membaca.

Judul : Relasi dan Fungsi: Grafik fungsi linier dan kuadrat
link : Relasi dan Fungsi: Grafik fungsi linier dan kuadrat

Relasi dan Fungsi: Grafik fungsi linier dan kuadrat

Pada pelajaran sebelumnya, kalian telah belajar tentang bagaimana menyelesaikan dan menggambar grafik fungsi linear & grafik fungsi kuadrat. Oleh karena itu, pada pelajaran ini, kalian akan belajar tentang bagaimana menentukan titik potong serta nilai maksimum dan minimum dari suatu fungsi dengan menggunakan grafik.

Ingatlah kembali metode menggambar grafik fungsi linear dan grafik fungsi kuadrat.
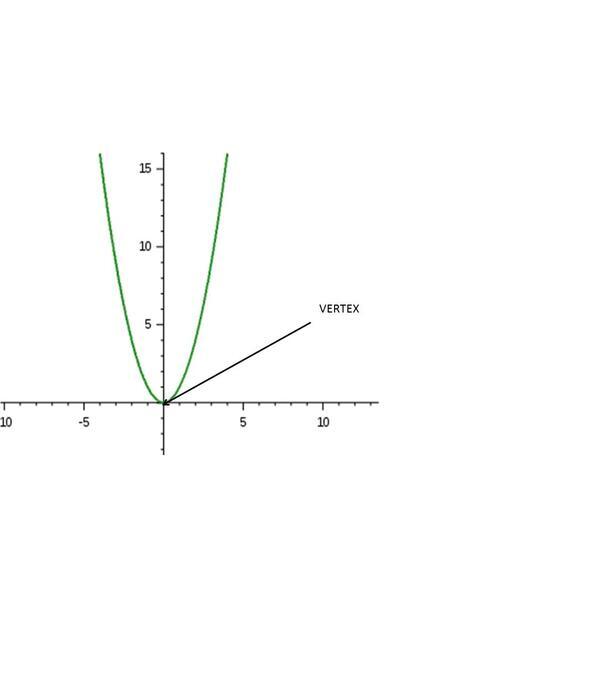
Grafik persamaan kuadrat y = ax²+ bx + c selalu berbentuk parabola. Sebagai contoh adalah grafik y = x².


Titik puncak dari suatu grafik fungsi kuadrat adalah titik yang terletak pada sumbu simetri, dimana titik tersebut dilalui oleh parabola. Selanjutnya, jika koefisien dari x² bernilai positif, maka titik puncaknya merupakan titik terendah dalam grafik. Akan tetapi, jika koefisien dari x² bernilai negatif, maka titik puncaknya merupakan titik tertinggi dalam grafik.

Nilai maksimum dari suatu fungsi kuadrat didefinisikan sebagai nilai terbesar yang dapat dicapai oleh fungsi kuadrat tersebut. Sedangkan nilai minimumnya didefinisikan sebagai nilai terkecil yang dapat dicapai oleh fungsi kuadrat tersebut.

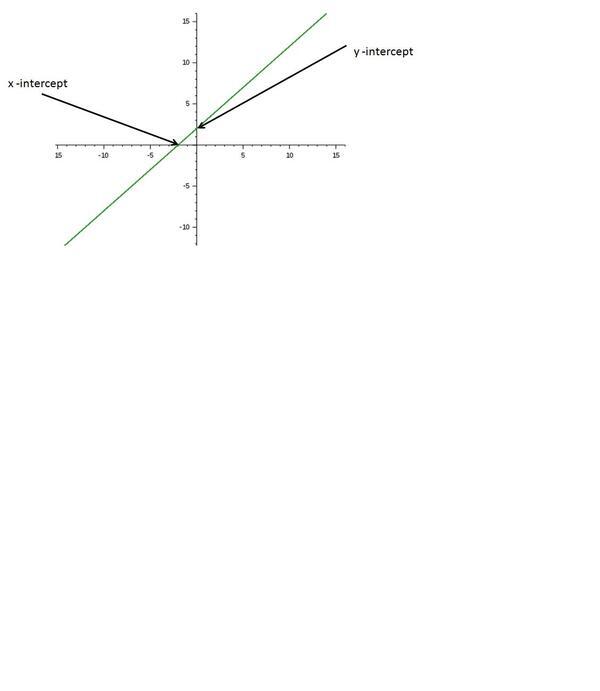
Grafik persamaan linear y = ax + b selalu berupa garis lurus. Sebagai contoh adalah grafik y = x + 2.



Absis dari titik potong dengan sumbu X diperoleh ketika y = 0. Sedangkan ordinat dari titik potong dengan sumbu Y diperoleh ketika x = 0.

Lebih lanjut, dalam pelajaran ini kalian akan belajar untuk menganalisa suatu grafik fungsi dan secara khusus akan belajar tentang bagaimana untuk :
       •menentukan nilai maksimum dan minimum serta titik potong dari suatu fungsi kuadrat                                          dengan menggunakan grafik
       •menentukan titik potong dari sutu persamaan dengan menggunakan grafik

Contoh 1 :

Gambarlah grafik y = 2x + 8 !
Selanjutnya, tentukan titik potong dengan sumbu X!

Penyelesaian :

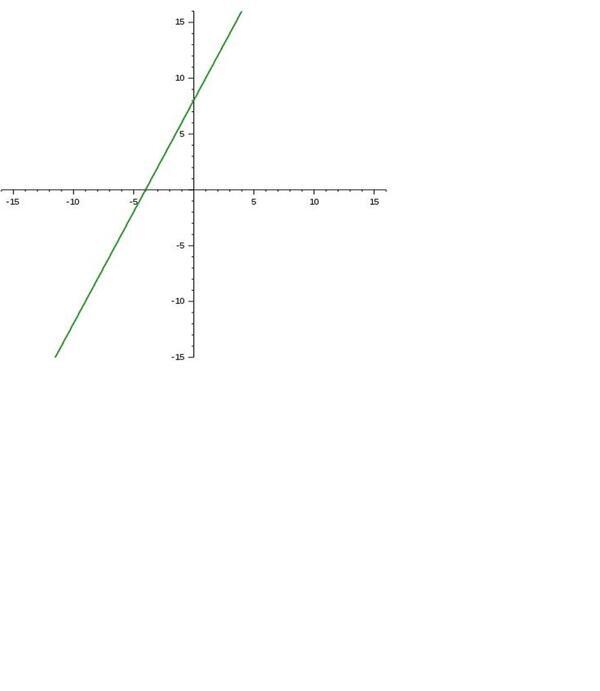
Perhatikan grafik y = 2x + 8 pada gambar di bawah!



Seperti yang terlihat pada grafik, nilai y = 0 saat x = -4.
Dengan demikian, titik potong grafik dengan sumbu X adalah (-4,0). Hal ini dapat diperiksa kebenarannya dengan cara mensubtitusikan y = 0 ke dalam persamaan.
                0 = 2x + 8
                x  = -4

Contoh 2 :
Gambarlah grafik y = (x-4)(x+4) dan tentukan titik potong antara grafik dengan sumbu Y!

Penyelesaian :

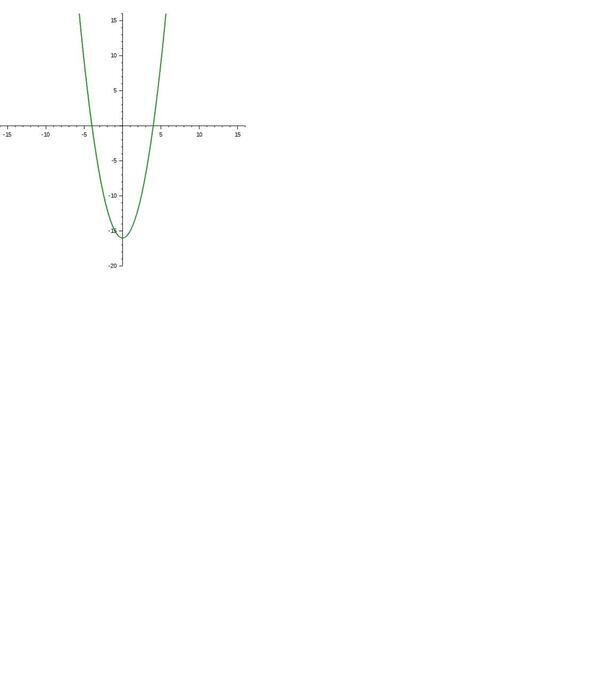
Perhatikan grafik y = (x-4)(x+4) pada gambar di bawah!



Seperti yang terlihat pada grafik, nilai x = 0 saat y = -16.
Dengan demikian, titik potong grafik dengan sumbu Y adalah (0,-16). Hal ini dapat diperiksa kebenarannya dengan cara mensubtitusikan x = 0 ke dalam persamaan.
                y = (0-4)(0+4)
                y = -16
Lebih lanjut, grafik tersebut akan mempunyai nilai minimum pada titik (0,-16). Hal ini terjadi karena titik tersebut merupakan titik terendah yang dapat dicapai oleh grafik.

Dengan demikian, dapat disimpulkan bahwa sebuah persamaan kuadrat hanya dapat mempunyai nilai maksimum atau minimum saja, tetapi tidak keduanya.

Demikian Relasi dan Fungsi: Grafik fungsi linier dan kuadrat

Sekianlah postingan Artikel Relasi dan Fungsi: Grafik fungsi linier dan kuadrat kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih

Anda sekarang membaca artikel Relasi dan Fungsi: Grafik fungsi linier dan kuadrat dengan alamat link https://metodekuadrat.blogspot.com/2016/06/relasi-dan-fungsi-grafik-fungsi-linier.html