Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel - Hallo semua metode kuadrat, Pada Postingan kali ini yang berjudul Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel, telah kami persiapkan dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Matematika, ini dapat anda pahami. dan bermanfaat, selamat membaca.

Judul : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel
link : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel

Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel

Sebuah sistem pertidaksamaan linear terdiri dari dua atau lebih pertidaksamaan yang mana batas-batas dari grafiknya merupakan garis lurus. Daerah penyelesaianuntuk sistem pertidaksamaan linear adalah daerah dari bidang yang diarsir secara berulang kali (beririsan). Setiap titik di daerah ini adalah penyelesaian dari sistem pertidaksamaan linear.

Untuk menemukan daerah penyelesaian, buatlah grafik dari semua pertidaksamaan pada suatu sistem koordinat yang sama, berhati-hatilah untuk mengarsir ruas yang benar dari setiap garis. Untuk menguji apakah suatu titik adalah penyelesaian dari sistem pertidaksamaan atau bukan, kita dapat memeriksa dengan cara melihat apakah titik tersebut terletak pada daerah yang diarsir berkali-kali (beririsan), atau kita bisa memasukkan koordinat titik ke setiap pertidaksamaan untuk melihat apakah titik tersebut memenuhi setiap pertidaksamaan yang ada.

Contoh 1

Gambarlah grafik dari sistem pertidaksamaan berikut dan tentukan apakah titik (1, -4) merupakan penyelesaian untuk sistem pertidaksamaan tersebut atau bukan.

Pertidaksamaan pertama dalam sistem digambarkan dengan garis merah muda, daerah yang diarsir berada di atas garis. Pertidaksamaan kedua digambarkan dengan garis hijau, daerah yang diarsir berada di atas garis. Dan pertidaksamaan ketiga digambarkan dengan garis biru, daerah yang diarsir berada di bawah garis. Daerah biru muda menunjukkan tempat di mana ketiga pertidaksamaan saling beririsan, ini adalah himpunan daerah penyelesaian yang untuk sistem ini.

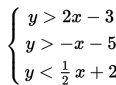
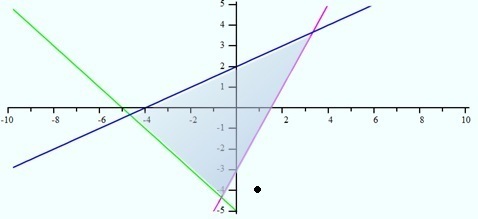
Sekarang kita ingin mengetahui apakah titik (1, -4) merupakan penyelesaian untuk pertidaksamaan ini atau bukan. Titik ini kita tandakan pada grafik, dan kita bisa melihat bahwa ia tidak berada di daerah biru muda, sehingga ia bukan merupakan penyelesaian. Cara lainnya, ini bisa diuji dengan memasukkan x = 1 dan y = -4 ke dalam ketiga pertidaksamaan. Kita akan melihat bahwa titik tersebut tidak memenuhi pertidaksamaan yang pertama.

Contoh 2

Tulislah sistem pertidaksamaan linear yang grafiknya ditunjukkan seperti di bawah ini.

Tulis setiap pertidaksamaan untuk empat garis yang diberikan. Garis merah muda memiliki persamaany = 4. Karena daerah penyelesaian diarsir pada bagian bawah garis ini, pertidaksamaan pertama adalahy< 4.

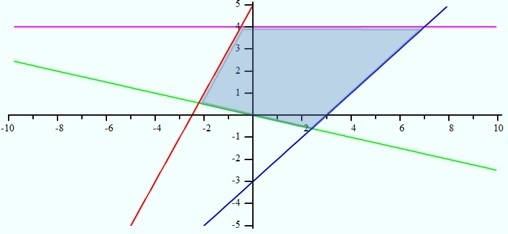
Garis merah memiliki titik potong dengan sumbu Y dengan ordinat 5 dan gradien 2, sehingga persamaan yang didapatkan adalahy = 2x + 5. Daerah yang diarsir berada di bawah garis ini, sehingga pertidaksamaan kedua adalahy< 2x + 5.

Garis hijau memiliki titik potong dengan sumbu Y dengan ordinat 0 dan gradien -½, sehingga persamaan yang didapatkan adalah y = -½ x . Daerah yang diarsir berada di atas garis ini, sehingga pertidaksamaan ketiga adalah y > - - x .

Garis biru memiliki titik potong dengan sumbu Y dengan ordinat -3 dan gradien 1, sehingga persamaan yang didapat adalah y = x – 3. Daerah yang diarsir berada di atas garis ini, sehingga pertidaksamaan keempat adalah y > x – 3.

Jadi, sistem pertidaksamaan yang ditunjukkan oleh grafik ini adalah:

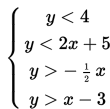
Demikian Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel

Sekianlah postingan Artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih

Anda sekarang membaca artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik Sistem Pertidaksamaan Linear Dalam Dua Variabel dengan alamat link https://metodekuadrat.blogspot.com/2016/06/sistem-persamaan-dan-pertidaksamaan_98.html