Judul : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik dari persamaan dengan dua variabel
link : Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik dari persamaan dengan dua variabel
Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik dari persamaan dengan dua variabel
Grafik persamaan dengan 2 variabel
Grafik persamaan dengan 2 variabel adalah himpunan solusi dari persamaan 2 variabel tersebut yang dinyatakan dalam bidang koordinat dan biasanya berbentuk kurva (walaupun bisa juga berbentuk garis).
 Ketika sebuah sistem persamaan dalam dua variabel diberikan, maka penyelesaiannya adalah titik yang memenuhi semua persamaan dalam sistem. Jika suatu sistem terdiri atas dua persamaan, maka penyelesaiannya dapat berupa : tepat satu penyelesaian, tidak ada penyelesaian, atau tak berhingga penyelesaian.
Ketika sebuah sistem persamaan dalam dua variabel diberikan, maka penyelesaiannya adalah titik yang memenuhi semua persamaan dalam sistem. Jika suatu sistem terdiri atas dua persamaan, maka penyelesaiannya dapat berupa : tepat satu penyelesaian, tidak ada penyelesaian, atau tak berhingga penyelesaian.

Contoh : 
Contoh : 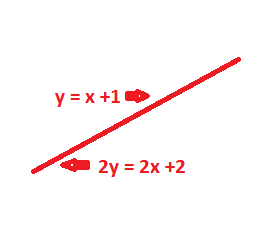 Untuk mencari penyelesaiannya, eliminasilah salah satu variabelnya, kemudian carilah nilai dari variabel yang tersisa. Untuk mencari titik potong, carilah nilai dari variabel yang telah dieliminasi, yaitu dengan melakukan subtitusi ke salah satu persamaan.
Untuk mencari penyelesaiannya, eliminasilah salah satu variabelnya, kemudian carilah nilai dari variabel yang tersisa. Untuk mencari titik potong, carilah nilai dari variabel yang telah dieliminasi, yaitu dengan melakukan subtitusi ke salah satu persamaan.
Grafik persamaan dengan 2 variabel adalah himpunan solusi dari persamaan 2 variabel tersebut yang dinyatakan dalam bidang koordinat dan biasanya berbentuk kurva (walaupun bisa juga berbentuk garis).
Menggambar persamaan linear adalah hal yang paling mudah. Contoh :
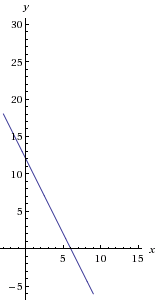
2x + y = 12
Langkah pertama : menentukan titik potong garis tersebut dengan sumbu X dan sumbu Y. Jika perhitungan kalian benar, maka akan diperoleh titik (6,0) dan (0,12). Selanjutnya, dengan menghubungkan kedua titikk potong tersebut dan memanjangkannya, diperoleh hasil sebagai berikut :

Kasus 1 : Tepat satu penyelesaian
Hal ini merupakan kejadian yang biasa terjadi. Adapun penyelesaiannya merupakan titik potong kedua garis yang mana hanya berpotongan tepat satu kali.
Kasus 2 : Tidak ada penyelesaian
Hal ini terjadi saat kedua garis saling sejajar.Contoh :
- Garis 1 : y = 4x +9
- Garis 2 : y = 4x + 5

Kasus 3 : Tak berhingga penyelesaian
Kasus ini jarang terjadi dan hanya terjadi jika kedua persamaan garis yang diberikan adalah sama.Contoh :
- Garis 1 : y = x + 1
- Garis 2 : 2y = 2x + 2
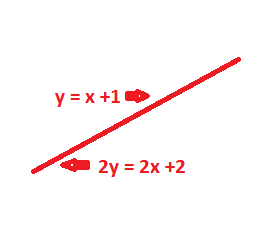
CONTOH 1 :
Dari pilihan berikut ini, garis manakah yang melalui titik (1,3)?
A) 2x - y = -1
B) 3x - y = 1
C) y = 3x +2
D) y = x/3
PENYELESAIAN :
Sebuah titik akan dilalui oleh suatu garis tertentu jika titik tersebut memenuhi persamaan garis tersebut. Dari contoh di atas, titik (1,3) hanya memenuhi persamaan garis 2x - y = -1. Oleh karena itu, opsi A adalah jawaban yang benar.
CONTOH 2 :
Tentukan titik potong antara garis y = x-1 dan lingkaran (x-1)2 + y2 = 50 !
A) (6,5) dan (-4,-5)
B) (-6,-5) dan (4,5)
C) (6,-5) dan (4,5)
D) (6,5) dan (-4,5)
PENYELESAIAN :
Dengan mensubtitusikan y = x-1 ke dalam persamaan lingkaran, maka diperoleh :
(x-1)2 + y2 = 50
(x-1)2 + (x-1)2 = 50
(x-1)2 = 25
x-1 = ±5
Dengan demikian, x = 6 atau x = -4.
Jika x = 6, maka y = x-1 = 5.
Jika x = -4, maka y = x-1 = -5.
Jadi, titik potong yang dicari adalah (6,5) dan (-4,-5).
Dengan kata lain, opsi B adalah jawaban yang benar.
CONTOH 3 :
Dari pernyataan berikut ini, manakah yang benar tentang kedudukan titik (2,3)?
A) Terletak pada lingkaran x2 + y2 = 42
B) Terletak di dalam lingkaran x2 + y2 = 42
C) Terletak di luar lingkaran x2 + y2 = 42
PENYELESAIAN :
Dengan melakukan subtitusi ke persamaan lingkaran, maka diperoleh : x2 + y2 = 42.
22 + 32 = 4 + 9 = 13 < 42
Dengan demikian, titik (2,3) terletak di dalam lingkaran. Dengan kata lain, opsi B adalah pilihan jawaban yang benar.
Demikian Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik dari persamaan dengan dua variabel
Sekianlah postingan Artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik dari persamaan dengan dua variabel kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel Sistem Persamaan dan Pertidaksamaan Linier Dua Variabel, dan Sistem Persamaan Linier Tiga Variabel: Grafik dari persamaan dengan dua variabel dengan alamat link https://metodekuadrat.blogspot.com/2016/06/sistem-persamaan-dan-pertidaksamaan_32.html