Relasi dan Fungsi: Membentuk Fungsi Linear - Hallo semua metode kuadrat, Pada Postingan kali ini yang berjudul Relasi dan Fungsi: Membentuk Fungsi Linear, telah kami persiapkan dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Matematika, ini dapat anda pahami. dan bermanfaat, selamat membaca.

Judul : Relasi dan Fungsi: Membentuk Fungsi Linear
link : Relasi dan Fungsi: Membentuk Fungsi Linear

Relasi dan Fungsi: Membentuk Fungsi Linear

Fungsi linear adalah fungsi yang dinyatakan dalam persamaan berbentuk f(x)
= kx + b; k adalah gradien garis. Bentuk persamaan ini disebut sebagai bentuk persamaan garis dengan gradien-titik potong. Jika k=0, garisnya sejajar dengan sumbu X.


   
Rumus umum lainnya adalah rumus titik-gradien. Jika gradien garis dan titik
(x₀, y₀)
pada garis tersebut diketahui, persamaan garis dapat dihitung sebagai berikut:
  y-
y₀=k(x-x₀)_.
Contoh 1. Tunjukkan
garis yang diperoleh dari persamaan y=(3/4)x+2.
Solusi.
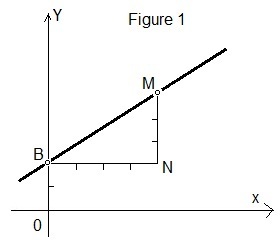
Pertama, kita tempatkan garis OB dari titik nol sepanjang sumbu Y, nilainya sama dengan 2 (lihat Gb.1). Kemudian, kita tarik garis datar BN dari titik B, panjangnya sama dengan 4. Langkah berikut adalah menarik segmen NM berupa garis vertikal
dari titik M dengan panjang 3. Dengan menggabungkan titik B dan M, kita
peroleh garis yang diminta.      Ketika
memikirkan grafik fungsi linear, kadang akan terbantu jika kita plot titik potong dengan sumbu x-
dan sumbu y.
Titik potong dengan sumbu X diperoleh jika y=0. Dalam fungsi linear, koordinat titik potong ini adalah (-b/k, 0). Titik potong dengan sumbu Y diperoleh jika x=0. Dalam fungsi linear, koordinat titik potong ini adalah (0, b).
Titik potong dengan sumbu x diperoleh jika y = 0. Dalam fungsi linear, koordinat titik potong ini adalah (-b/k, 0).
Titik potong dengan sumbu y diperoleh jika x = 0. Dalam fungsi linear, koordinat
titik potong ini adalah (0, b). Contoh 2.
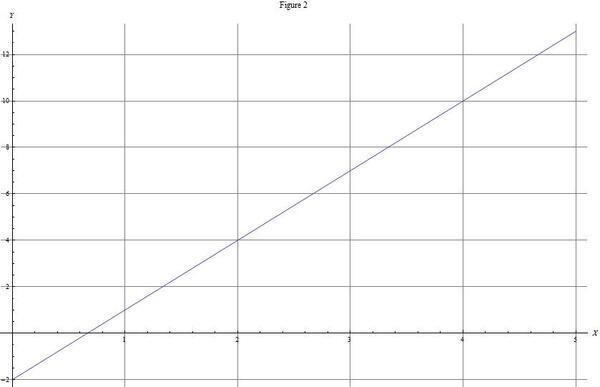
Tuliskan persamaan garis yang ditunjukkan dalam Gambar 2 (lihat Gb.2).
Solusi.
Titik potong y dari grafik itu
terjadi pada titik x sama dengan nol. Pada fungsi yang diberikan, berupa titik (0, -2). Jadi, b = -2. Untuk mencari k, mari kita hitung nilai tangen sudut segitiga dengan titik sudut (2,4), (4,4), (4,10). Grafik ini memiliki cathetus c dan d dengan panjang 6 dan 2. Jadi, sebagaimana diketahui dari trigonometri

Catatan 1.
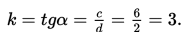
Jika garisnya vertikal, persamaannya tampak seperti x=a, dan a adalah konstanta.
Jika kita tahu bahwa koordinat dari dua titik merupakan bagian dari garis tersebut, persamaannya adalah:
y−y1y2−y1=x−x1x2−x1Substitusikan koordinat titik M dan N ke dalam persamaan garis, dengan dua titik itu kita peroleh apa yang diminta

Catatan 2.
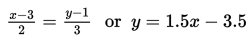
Fungsi linear dapat dibentuk
dengan menggunakan dua pasang bilangan, yang disajikan dalam bentuk tabel:

Demikian Relasi dan Fungsi: Membentuk Fungsi Linear

Sekianlah postingan Artikel Relasi dan Fungsi: Membentuk Fungsi Linear kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih

Anda sekarang membaca artikel Relasi dan Fungsi: Membentuk Fungsi Linear dengan alamat link https://metodekuadrat.blogspot.com/2016/06/relasi-dan-fungsi-membentuk-fungsi.html