Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks - Hallo semua metode kuadrat, Pada Postingan kali ini yang berjudul Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks, telah kami persiapkan dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Matematika, ini dapat anda pahami. dan bermanfaat, selamat membaca.

Judul : Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks
link : Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks

Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks

Sebuah persamaan kuadrat ditulis sebagai

di mana

Fungsi kuadrat induk adalah;

y=ax2

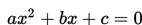
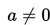
Grafik dari fungsi kuadrat berbentuk parabola. Beberapa istilah yang terkait dengan parabola diberikan di bawah ini 

Titik puncak: titik tertinggi (nilai maksimum) atau titik terendah (nilai minimum) pada grafik.

Sumbu simetri: Sebuah garis yang melalui titik puncak dan membagi parabola menjadi dua bagian yang simetris.

Jika a positif, maka parabola terbuka ke atas

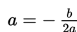
Jika a negatif, maka parabola terbuka ke bawah

Jika a>1, maka parabola terbuka dengan cepat (grafik sempit) dan jika a<1, maka parabola terbuka perlahan (grafik lebar). Untuk menggambar grafik kuadrat, seseorang dapat membuat tabel-T dengan memilih nilai yang sesuai untuk x dan memasukkannya untuk mencari nilai y. Juga untuk menemukan titik puncak dan sumbu simetri.

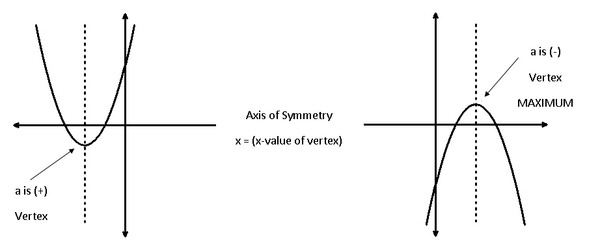
Contoh: Untuk fungsi 

y=4x2−3x+7

Sumbu simetri,

Titik puncak: (masukkan x ke dalam persamaan)

y=4(38)−3(38)+7y=4(964)−3(38)+7y=10316

Jadi titik puncak adalah, (1/4, 103/16)

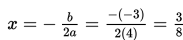
Grafik kuadrat dalam bentuk titik potong adalah: 

Dimana p dan q adalah titik potong dengan x. Sumbu simetri berada di tengah-tengah antara p dan q, yaitu    x = (p+q)/2

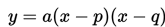
Bagaimana kita menggambar grafik bentuk titik potong? Jawabannya adalah 

1. Cari titik potong dengan sumbu x. 

2. Temukan titik puncak. 

3. Gambar parabola melalui titik potong dan titik puncak

Bentuk titik puncak dari kuadratik: 

          

Empat bentuk kuadratik:-

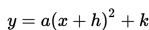
1. Pencerminan atas sumbu X :

(a) Jika a negatif, maka parabola akan menunjuk ke bawah.

(b) Jika a positif, maka parabola akan menunjuk ke atas.

2. Peregangan atau penyusutan vertikal:

(a) Jika a >1, maka parabola akan tinggi dan sempit. Dan jika a adalah antara 0 dan 1, maka parabola akan pendek dan lebar.

3. Pergeseran ke kiri dan kanan: Jika 'h' adalah negatif maka parabola akan berpindah ke kanan sejauh h satuan, dan jika positif maka akan berpindah ke kiri sejauh h satuan.

4. Pergeseran ke atas dan ke bawah: Jika 'k' adalah positif maka parabola akan berpindah ke atas sejauh k satuan, dan jika negatif maka akan berpindah ke bawah sejauh k satuan.

Menyelesaikan fungsi kuadrat dengan melengkapkan kuadrat untuk menunjukkan nol:

f(x)=ax2+bx+cf(x)=a(aax2+cf(x)=a(x2+bax+(b2÷−(b2÷)+cf(x)=a(x2+bax+(b2a)−(b2a))+cf(x)=a(x2+bax+b24a2−b24a2)+cf(x)=a(x2+bax+b24a2)+a(−b24a2)+cf(x)=a(x2+bax+b24a2)−b24a+cf(x)=a(x+−b24a+4ac4af(x)=a(x++4ac−b24a

Untuk menyelesaikan nol dari fungsi kuadrat f kita mengatur variabel terikat (x) sebagai sama dengan nol dan mencari penyelesaian untuk variabel bebas

f(x)=a(x+b2a)2+4ac−b24a=0

Pernyataan terakhir di atas  disebut sebagai rumus kuadrat dan berguna untuk menentukan akar dari fungsi kuadrat, terutama ketika fungsi itu tidak mudah  difaktorkan.

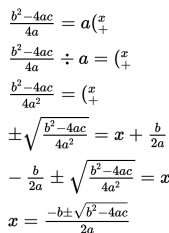
Misalnya dalam menemukan nol dari

y=−2x2+8x−3

kita harus menetapkan y = 0 dan mencari penyelesaian untuk x

Bandingkan dengan

ax2+bx+c=0

a= - 2,   b=8, c= -3

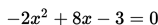
Substitusikan nilai-nilai berikut dalam rumus fungsi kuadrat:

Fungsi kuadrat ini terbuka ke bawah karena a<0 dan melalui sumbu X pada sekitar 0,42 dan 3,58, titik puncak berada di atas sumbu X

Soal latihan: -

Bagian 1: Untuk masing-masing fungsi yang diberikan di bawah ini, lakukan tiga perintah berikut:

1. Tulislah koordinat dari titik puncak

2.Buatlah sketsa yang akurat di atas kertas grafik

3. Tulislah persamaan garis simetri

1. f(x) = x2+32. f(x)=2x2−53.  f(x)=(x-2)2−44.  f(x)=12(x+1)25.  f(x)=−12(x-5)2+26.  f(x)=−7−(x+1)2

Bagian 2: Jawablah setiap pertanyaan berikut

7. Grafik dari 

f(x) = x2

Telah ditransformasikan sehingga garis simetrinya adalah  x= - 2 dan telah bergeser naik sampai 13 satuan. Tentukan titik puncaknya.

8.   Grafik dari 

Telah ditransformasikan sehingga titik puncak yang masih tetap (0, 0), tapi sekarang melalui titik (1, 3). Bagaimanakah persamaan yang baru sekarang ?

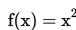
9. Grafik dari

f(x) = x2

Telah bergeser ke kiri sejauh 3,5 satuan, naik ke atas sejauh 1,5 satuan dan berubah bentuknya sehingga terbuka ke bawah. Bagaimanakah persamaan yang baru sekarang?

10. Grafik dari  

Telah ditransformasikan sehingga titik puncaknya menjadi (5, - 10), terbuka ke atas dan sekarang menjadi tepat dua kali lebih curam. Bagaimanakah persamaan yang baru sekarang?

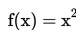
11. Carilah X (dengan  menggunakan bentuk-bentuk khusus dari persamaan kuadrat)

(a)  x2=−1               (b)   x2−1=0     (c)   x2−7x=0         (d)   x2−3x=0

1.  Carilah penyelesaian untuk x

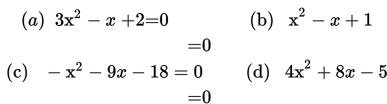
1. Tuliskan kembali persamaan kuadrat berikut dalam bentuk faktor
   
   

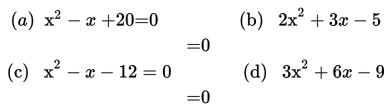
Demikian Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks

Sekianlah postingan Artikel Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih

Anda sekarang membaca artikel Persamaan dan Fungsi Kuadrat: Grafik Kuadratik Dalam Konteks dengan alamat link https://metodekuadrat.blogspot.com/2016/06/persamaan-dan-fungsi-kuadrat-grafik.html