Judul : Geometri: Jarak Titik ke Garis
link : Geometri: Jarak Titik ke Garis
Geometri: Jarak Titik ke Garis
Beberapa waktu yang lalu kalian telah mempelajari materi tentang hubungan antara titik dengan garis, yaitu titik terletak pada garis atau titik di luar garis.
Untuk kedudukan titik yang terletak di luar garis tentunya dia mempunyai jarak. Dalam topik ini kita akan mempelajari topik jarak antara titik dan garis.
Apa kalian masih ingat cara mencari jarak antara dua titik?
1. Proyeksi sebuah titik T pada sebuah garis g dapat diperoleh dengan menarik garis tegak lurus dari titik T terhadap garis g.
2. Perpotongan garis tegak lurus dari titik T dengan garis g yaitu titik T', disebut proyeksi titik T pada garis g.
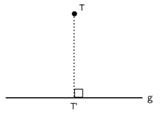T' adalah proyeksi T pada garis g
3. Jarak antara titik T dan garis g adalah panjang ruas garis yang tegak lurus dari titik T ke garis g atau panjang ruas garis lurus dari titik T ke titik proyeksinya di T' pada garis g.
d adalah jarak antara titik T dan garis g
4. Untuk menghitung jarak antara titik T dan garis g dibuat segitiga yang memuat titik T dan garis g , kemudian dapat digunakan rumus :
a) teorema Pythagoras, jika segitiga yang terbentuk segitiga sama kaki
b) luas segitiga, jika segitiga yang terbentuk segitiga siku-siku
c) trigonometri, jika segitiga yang terbentuk segitiga sembarang
Untuk lebih jelasnya, mari kita perhatikan contoh berikut.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung jarak
a) titik A dan garis BD
b) titik A dan garis HF
c) titik A dan garis HB
Jawab :
a)
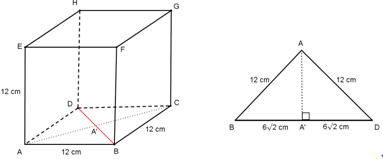Untuk menghitung jarak antara titik A dan garis BD dibuat ∆ABD (segitiga sama kaki), kemudian dibuat proyeksi titik A pada garis BD yaitu A’, maka jarak titik A dan garis BD adalah AA’.
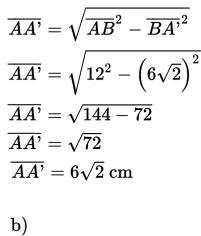
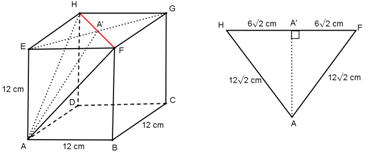Untuk menghitung jarak titik A dan garis HF dibuat ∆AFH (segitiga sama kaki), kemudian dibuat proyeksi titik A pada garis HF yaitu A’, maka jarak titik A dan garis HF adalah AA’.
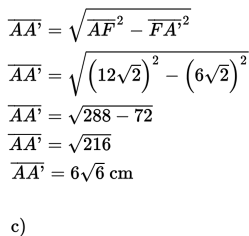
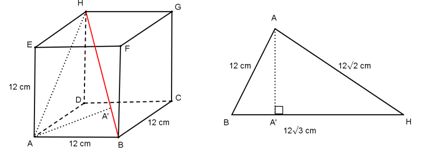Untuk menghitung jarak titik A dan garis HB dibuat ∆HAB (segitiga siku-siku di A), kemudian dibuat proyeksi titik A pada garis HB yaitu A’, maka jarak titik A dan garis HB adalah AA’.
Untuk kedudukan titik yang terletak di luar garis tentunya dia mempunyai jarak. Dalam topik ini kita akan mempelajari topik jarak antara titik dan garis.
Apa kalian masih ingat cara mencari jarak antara dua titik?
1. Proyeksi sebuah titik T pada sebuah garis g dapat diperoleh dengan menarik garis tegak lurus dari titik T terhadap garis g.
2. Perpotongan garis tegak lurus dari titik T dengan garis g yaitu titik T', disebut proyeksi titik T pada garis g.
3. Jarak antara titik T dan garis g adalah panjang ruas garis yang tegak lurus dari titik T ke garis g atau panjang ruas garis lurus dari titik T ke titik proyeksinya di T' pada garis g.
4. Untuk menghitung jarak antara titik T dan garis g dibuat segitiga yang memuat titik T dan garis g , kemudian dapat digunakan rumus :
a) teorema Pythagoras, jika segitiga yang terbentuk segitiga sama kaki
b) luas segitiga, jika segitiga yang terbentuk segitiga siku-siku
c) trigonometri, jika segitiga yang terbentuk segitiga sembarang
Untuk lebih jelasnya, mari kita perhatikan contoh berikut.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm.
Hitung jarak
a) titik A dan garis BD
b) titik A dan garis HF
c) titik A dan garis HB
Jawab :
a)
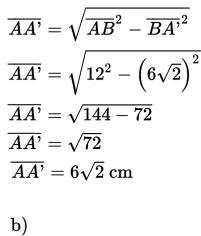
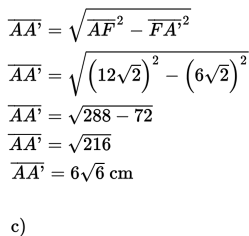
Demikian Geometri: Jarak Titik ke Garis
Sekianlah postingan Artikel Geometri: Jarak Titik ke Garis kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel Geometri: Jarak Titik ke Garis dengan alamat link https://metodekuadrat.blogspot.com/2016/06/geometri-jarak-titik-ke-garis.html
