Judul : Geometri: Hubungan antara Garis dan Garis
link : Geometri: Hubungan antara Garis dan Garis
Geometri: Hubungan antara Garis dan Garis
Setelah kemarin kita telah mempelajari hubungan antara titik dan garis serta hubungan antara titik dan bidang, sekarang kita akan mempelajari hubungan garis dengan garis.
Pokok materi ini nantinya akan kita gunakan untuk menghitung jarak antara dua garis sejajar atau dua garis bersilangan, ataupun untuk menghitung besar sudut antara dua garis yang berpotongan atau bersilangan.
Apa kalian masih ingat dengan apa yang dimaksud garis?
Mari kita coba ingat kembali tentang pengertian garis.
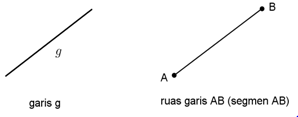
Garis adalah himpunan titik-titik yang tidak terbatas banyaknya. Garis (garis lurus) memiliki ukuran panjang tetapi tidak mempunyai ukuran lebar. Biasanya garis hanya dilukiskan sebagian saja, disebut wakil garis. Nama wakil garis dilambangkan dengan huruf kecil (g, h, k) atau menyebutkan nama segmen garis dari titik pangkal ke titik ujung.
Contoh :
Dua Garis Berpotongan
Dua garis dikatakan berpotongan, jika kedua garis tersebut terletak pada satu bidang dan memiliki sebuah titik potong.
Apabila kedua garis tersebut berpotongan pada lebih dari satu titik potong maka kedua garis itu dinamakan berhimpit.
Dua Garis Sejajar
Dua garis dikatakan sejajar, jika kedua garis tersebut terletak pada satu bidang dan tidak memiliki titik potong.
Aksioma Dua Garis Sejajar
Aksioma 1 :
Melalui sebuah titik yang berada di luar suatu garis hanya dapat dibuat satu garis yang sejajar dengan garis tersebut
Dalil tentang Dua Garis Sejajar
Dalil 2 :
Jika garis sejajar dengan garis dan garis sejajar dengan garis, maka garis sejajar dengan garis
Dalil 3 :
Jika garis sejajar garis dan memotong garis, garis sejajar garis dan memotong garis , maka garis-garis , dan terletak pada satu bidang
Dalil 4 :
Jika garis sejajar garis sedangkan garis menembus bidang, maka garis juga menembus bidang
Dua Garis Bersilangan
Dua garis dikatakan bersilangan, jika kedua garis tidak terletak pada bidang yang sama atau apabila pada kedua garis tersebut tidak dapat dibuat sebuah bidang yang melalui kedua garis tersebut.
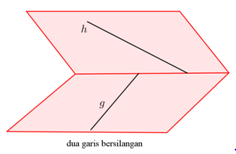
Untuk lebih memahami konsep hubungan antara dua garis, mari kita perhatikan contoh berikut :
Contoh :
Diketahui kubus PQRS.TUVW
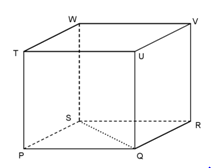Tentukan kedudukan garis-garis berikut :
Jawab :
Pokok materi ini nantinya akan kita gunakan untuk menghitung jarak antara dua garis sejajar atau dua garis bersilangan, ataupun untuk menghitung besar sudut antara dua garis yang berpotongan atau bersilangan.
Apa kalian masih ingat dengan apa yang dimaksud garis?
Mari kita coba ingat kembali tentang pengertian garis.
Garis adalah himpunan titik-titik yang tidak terbatas banyaknya. Garis (garis lurus) memiliki ukuran panjang tetapi tidak mempunyai ukuran lebar. Biasanya garis hanya dilukiskan sebagian saja, disebut wakil garis. Nama wakil garis dilambangkan dengan huruf kecil (g, h, k) atau menyebutkan nama segmen garis dari titik pangkal ke titik ujung.
Contoh :
Dua Garis Berpotongan
Dua garis dikatakan berpotongan, jika kedua garis tersebut terletak pada satu bidang dan memiliki sebuah titik potong.
Apabila kedua garis tersebut berpotongan pada lebih dari satu titik potong maka kedua garis itu dinamakan berhimpit.
Dua Garis Sejajar
Dua garis dikatakan sejajar, jika kedua garis tersebut terletak pada satu bidang dan tidak memiliki titik potong.
Aksioma Dua Garis Sejajar
Aksioma 1 :
Melalui sebuah titik yang berada di luar suatu garis hanya dapat dibuat satu garis yang sejajar dengan garis tersebut
Dalil tentang Dua Garis Sejajar
Dalil 2 :
Jika garis sejajar dengan garis dan garis sejajar dengan garis, maka garis sejajar dengan garis
Dalil 3 :
Jika garis sejajar garis dan memotong garis, garis sejajar garis dan memotong garis , maka garis-garis , dan terletak pada satu bidang
Dalil 4 :
Jika garis sejajar garis sedangkan garis menembus bidang, maka garis juga menembus bidang
Dua Garis Bersilangan
Dua garis dikatakan bersilangan, jika kedua garis tidak terletak pada bidang yang sama atau apabila pada kedua garis tersebut tidak dapat dibuat sebuah bidang yang melalui kedua garis tersebut.
Untuk lebih memahami konsep hubungan antara dua garis, mari kita perhatikan contoh berikut :
Contoh :
Diketahui kubus PQRS.TUVW
- PS dan QS
- WS dan QR
- TU dan VW
Jawab :
- Pada gambar terlihat garis PS dan QS berpotongan di titik S, sehingga dikatakan kedudukan garis PS dan QS adalah berpotongan.
- Pada gambar terlihat garis WS dan QR tidak berada pada satu bidang yang sama atau antara garis WS dan QR tidak dapat dibuat sebuah bidang yang melalui kedua garis tersebut, sehingga dikatakan kedudukan garis WS dan QR adalah bersilangan.
- Pada gambar terlihat garis TU dan VW terletak pada satu bidang dan tidak memiliki titik potong, sehingga dikatakan kedudukan garis TU dan VW adalah sejajar.
Demikian Geometri: Hubungan antara Garis dan Garis
Sekianlah postingan Artikel Geometri: Hubungan antara Garis dan Garis kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel Geometri: Hubungan antara Garis dan Garis dengan alamat link https://metodekuadrat.blogspot.com/2016/06/geometri-hubungan-antara-garis-dan-garis.html
