Judul : Perbandingan Trigonometri Pada Segitiga Siku-Siku
link : Perbandingan Trigonometri Pada Segitiga Siku-Siku
Perbandingan Trigonometri Pada Segitiga Siku-Siku
Pada topik sebelumnya, kalian mempelajari ukuran suatu sudut. Nah, dalam topik ini kalian akan mempelajari perbandingan trigonometri suatu sudut dalam segitiga siku-siku.Apakah kalian masih ingat dengan sudut lancip?
Ya, sudut lancip berada di antara 0° dan 90°.
Mari kita gambar sudut lancip KAL.
- Pada garis AK, ambil sebarang titik, misal titik B dan gambarlah BC yang tegak lurus terhadap AL, sehingga terbentuk segitiga siku-siku BCA.
- Ambil lagi sebarang titik, misalnya titik D pada garis AK, kemudian gambarlah DE yang tegak lurus AL sehingga terbentuk segitiga siku-siku DEA.
- Ambil lagi sebarang titik, misalnya titik F pada garis AK, kemudian dan gambarlah FG yang tegak lurus AL, sehingga terbentuk segitiga siku-siku FGA begitu seterusnya.
Berdasarkan gambar di atas, jika kita menggunakan konsep kesebangunan, maka akan kita peroleh hubungan sebagai berikut:
Ternyata perbandingan untuk sudut A dapat kita tentukan dengan melihat ∆AKL, ∆ABC, ∆ADE, ∆AFG, maupun ∆AHI.
Selanjutnya, mari kita perhatikan segitiga ABC berikut.
Pada gambar tersebut, jika kita memandang dari sudut α, maka
- BC disebut sisi siku-siku di depan sudut α
- AB disebut sisi siku-siku kaki sudut α
- AC disebut hipotenusa
Sebelum kalian mempelajari tentang nilai perbandingan trigonometri, ada beberapa notasi yang perlu kalian ketahui, yaitu
- sinus α ditulis dengan notasi sin α
- kosinus α ditulis dengan notasi cos α
- tangen α ditulis dengan notasi tan α atau tg α
Sangat mudah untuk diingat bukan?
Nah, definisi nilai perbandingan trigonometri dari sudut α sebagai berikut:
Selain ketiga perbandingan di atas, kalian juga akan mempelajari perbandingan trigonometri yang lain, yaitu
- kotangen α → cot α atau ctg α
- sekan α → sec α
- kosekan → cosec α atau csc α
Berdasarkan perbandingan trigonometri tersebut, dapat kita temukan hubungan yang lain, yaitu
CONTOH SOAL
Apakah kalian sudah jelas dengan uraian materi tersebut?Agar kalian semakin memahami dalam mempelajari nilai perbandingan trigonometri, perhatikan beberapa contoh berikut ini.
Contoh 1:
Tentukan nilai sinus, kosinus dan tangen dari sudut-sudut lancip pada segitiga berikut.
Penyelesaian:
Pada segitiga ABC, panjang sisi AC (hipotenusa) belum diketahui.
Ingatkah kalian bagaimana cara menentukannya?
Dalam menentukan panjang sisi AC, dapat digunakan teorema Pythagoras.
Dengan demikian, gambar di atas bisa dilengkapi sehingga menjadi gambar berikut.
Dalam gambar di atas, sudut lancip dalam segitiga ABC adalah sudut α dan β.
Perbandingan trigonometri dari sudut α sebagai berikut:
Adapun perbandingan trigonometri dari sudut β sebagai berikut:
Contoh 2:
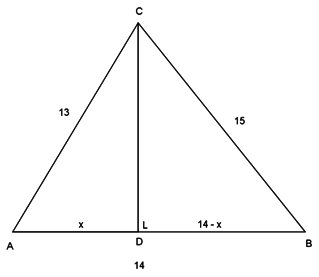
Perhatikan gambar berikut.
Hitunglah nilai sinus, kosinus dan tangen untuk sudut A dan B.
Penyelesaian:
Agar penyelesaian soal lebih mudah, dapat dibuat sketsa sebagai berikut.
Pada segitiga siku-siku ADC,
CD2 = 132 -x2 … (1)
Pada segitiga siku-siku BDC,
CD2 = 152 - (14 - x)2 … (2)
Selanjutnya, dari kedua persamaan di atas kita peroleh hasil sebagai berikut:
Dengan begitu, panjang AD adalah 5 satuan dan panjang DB adalah 9 satuan.
Selanjutnya, jika kita subtitusikan x = 5 ke persamaan (1), maka dapat kita tentukan panjang CD adalah 12 satuan.
Jadi, dapat kita simpulkan bahwa perbandingan trigonometri untuk sudut A pada segitiga di atas sebagai berikut:
Demikian Perbandingan Trigonometri Pada Segitiga Siku-Siku
Sekianlah postingan Artikel Perbandingan Trigonometri Pada Segitiga Siku-Siku kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel Perbandingan Trigonometri Pada Segitiga Siku-Siku dengan alamat link https://metodekuadrat.blogspot.com/2016/05/perbandingan-trigonometri-pada-segitiga.html
