Judul : EKSPONEN DAN LOGARITMA: Perhitungan dalam bentuk akar
link : EKSPONEN DAN LOGARITMA: Perhitungan dalam bentuk akar
EKSPONEN DAN LOGARITMA: Perhitungan dalam bentuk akar
Penghitungan dengan bentuk akar
Kalian sudah belajar cara menulis akar kuadrat dari suatu bilangan. Contoh :

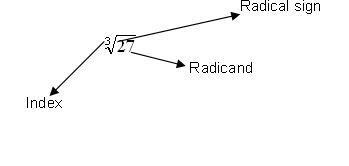
Akar pangkat tiga dari 27 dinyatakan dengan
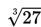
Akar pangkat empat dari 48 dinyatakan dengan
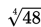
Ingat lagi, akar kuadrat dari
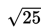
adalah 5, dan akar pangkat tiga dari
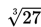
adalah 3.
Menyederhanakan kuadrat sempurna dan pangkat tiga sempurna memang mudah, tetapi tidak mudah menyederhanakan bilangan yang bukan bilangan kuadrat sempurna maupun bilangan pangkat tiga sempurna. Kita bisa saja memiliki bilangan dan variabel sebagai radikan.
Misalnya,
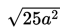
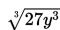
Kita bisa menyederhanakan bilangan dan variabel tersebut dengan menguraikannya menjadi bilangan yang lebih kecil. Jika bilangan radikan memiliki akar kuadrat, kita harus mencari suku (bilangan dasar) yang dapat dikalikan sebanyak pangkatnya sehingga mudah menyederhanakannya.
Misalnya,
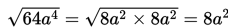
Jika suatu bilangan radikan berbentuk akar pangkat tiga, kita harus mengalikan bilangan dasar (suku) dari radikan tersebut sebanyak tiga kali.
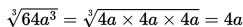
Contoh 1
Sederhanakan
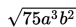
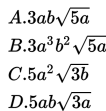
Ingat,
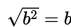
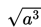
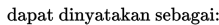
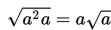

dapat dinyatakan sebagai
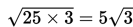
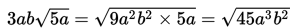
yang tidak sama dengan
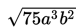
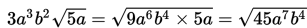
yang tidak sama dengan
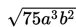
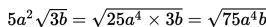
yang tidak sama dengan
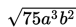
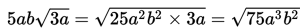
D benar.
2) Peter menggambar sebuah bujur sangkar dengan panjang 4 cm. Berapa panjang diagonal bujur sangkar tersebut?
Bujur sangkar yang digambar oleh Peter dapat ditunjukkan dengan diagram berikut ini:
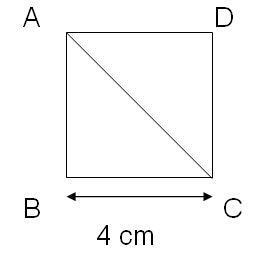
Penjelasan
Gunakan teorema Pythagoras untuk menghitung panjang diagonal tersebut.
Rumus
(AC)2 = (AB)2 + (BC) 2
(AC)2 = (4)2 + (4) 2
(AC)2 = 16 + 16
(AC)2 = 32
AC =
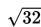
AC =
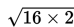
AC =
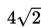
Jadi, panjang diagonal tersebut adalah:
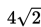
cm
Demikian EKSPONEN DAN LOGARITMA: Perhitungan dalam bentuk akar
Sekianlah postingan Artikel EKSPONEN DAN LOGARITMA: Perhitungan dalam bentuk akar kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, jangan lupa berkunjung kembali untuk postingan artikel lainnya, dan Terima kasih
Anda sekarang membaca artikel EKSPONEN DAN LOGARITMA: Perhitungan dalam bentuk akar dengan alamat link https://metodekuadrat.blogspot.com/2016/05/eksponen-dan-logaritma-perhitungan.html